Division

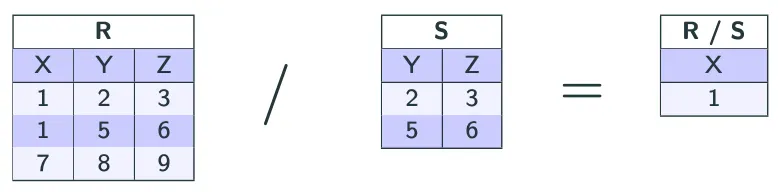
La division

• Opérandes :
  • Une relation R de schéma X
  • Une relation S de schéma Y
• Résultat :
  • une relation T de schéma X - Y (les attributs de Y sont retirés de X)
  • ne contenant aucune des lignes (v1, v2,..., vn)
  • telles que pour chaque ligne (w1, w2,..., wn) de S
  • R contient les lignes (v1, v2,..., vn, w1, w2,..., wn)
• Notation : R / S

---

La division

Théorie de la division

La division de R1 par R2 :

• sachant que R1 et R2 ont au moins un attribut commun (de même nom et domaine)

produit une relation R3 :

• qui comporte les attributs appartenant à R1 mais n’appartenant pas à R2
• et l’ensemble des tuples (lignes), qui concaténés à ceux de R2 donnent toujours un tuple de R1

Exemples de division

Exemples de requêtes de division

Soients les relations suivantes :

ETUDIANT (NUMET , NOM, PRENOM)
MATIERE (NUMMAT, LIBELLE)
EPREUVE (NUMEPR , NUMMAT, DATE)
INSCRIPTION (NUMET, NUMMAT)
RESULTAT (NUMET, NUMEPR , NOTE)

Questions

• Quels sont les étudiants inscrits dans toutes les matières ?
• Quels sont les étudiants ayant une note à chacune des épreuves ?

---

Exemples de requêtes de division

Quels sont les étudiants inscrits dans toutes les matières ?

INSCRIPTION / MATIERE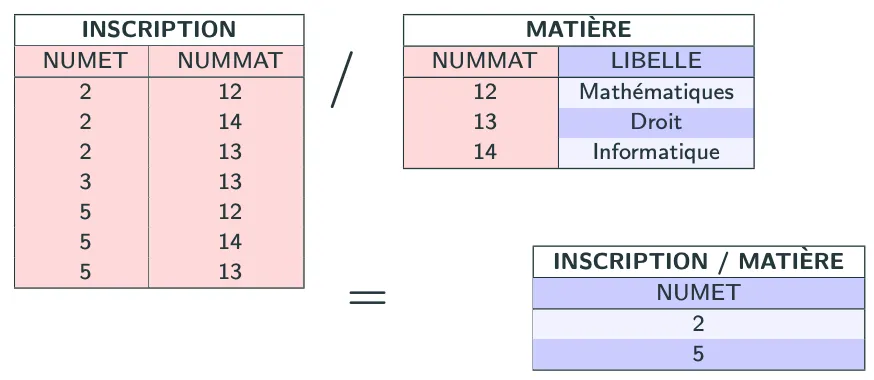

---

Exemples de requêtes de division

Quels sont les étudiants ayant une note à chacune des épreuves ?

RESULTAT / EPREUVE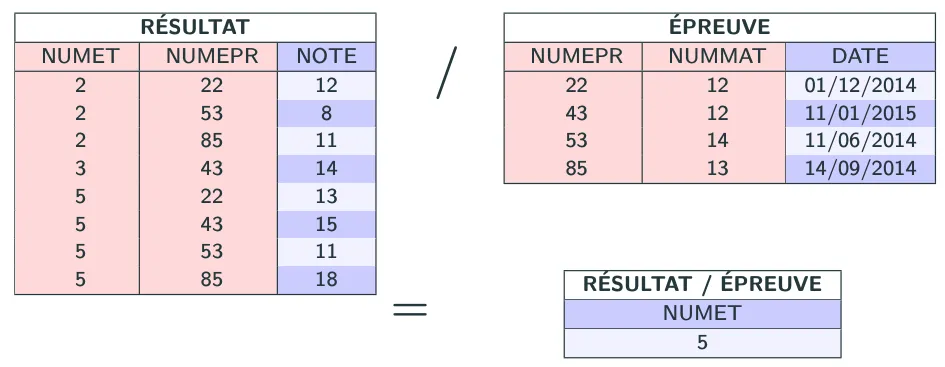

La division + une jointure

La division + une jointure

Si l’on veut maintenant les noms et prénoms des étudiants ayant obtenus une note à chacune des épreuves :

R = RESULTAT / EPREUVE
S = ETUDIANT[ NUMET, NOM, PRENOM ]
R (R.NUMET = S.NUMET) X S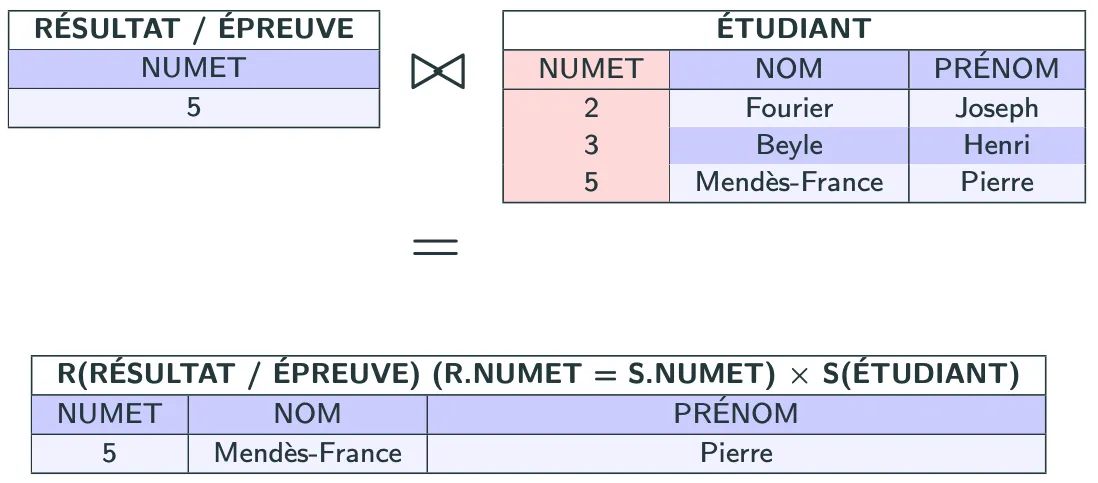

Conclusion sur la division

Conclusion sur la division

• La division est une opération complexe et peu intuitive
• Cependant, elle est très utile pour certaines requêtes qui sont difficiles à implémenter en SQL
  • Par exemple, les requêtes de type “pour tous” ou “pour chaque”
  • En SQL, il n’existe pas d’opérateur de division, il faut utiliser des jointures complexes pour simuler la division
  • Il sera donc souvent plus simple de réaliser ces requêtes d’abord en algèbre relationnelle avant de les traduire en SQL
• En algèbre relationnelle, la division est notée R / S